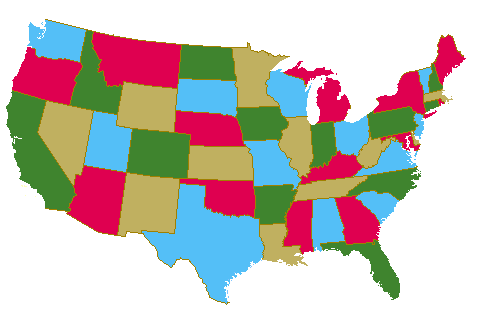
4색 지도 채색 문제: 지도 상의 여러 나라를 인접한 나라의 색이 다르도록 색칠하는데 4 색이면 충분한가?
증명은 되었지만 아직까지 간단한 증명이 발견되지 않은 문제. Koch 등이 1976년, 이 문제를 1936가지의 경우로 나눈 후에 이걸 컴퓨터로 1200 시간을 돌린 후에 4색으로 칠할 수 있다고 증명하긴 했다. 엄밀한 수학자는 펜과 종이를 사용하지 않은 이런 증명은 증명으로 취급하기를 꺼리기도 한다. 현재도 그리 나은 증명은 나오지 않았다. 경우의 수를 633가지로 줄인 것을 빼고는.
이 증명은 컴퓨터를 증명의 도구로 쓴 가장 대표적인 결과이다
증명은 되었지만 아직까지 간단한 증명이 발견되지 않은 문제. Koch 등이 1976년, 이 문제를 1936가지의 경우로 나눈 후에 이걸 컴퓨터로 1200 시간을 돌린 후에 4색으로 칠할 수 있다고 증명하긴 했다. 엄밀한 수학자는 펜과 종이를 사용하지 않은 이런 증명은 증명으로 취급하기를 꺼리기도 한다. 현재도 그리 나은 증명은 나오지 않았다. 경우의 수를 633가지로 줄인 것을 빼고는.
컴퓨터를 썼다고 이 증명이 틀린 것은 아니다. 그리고, 이 증명은 컴퓨터를 사용하긴 했지만, 경우의 수를 633가지로 나누는 데는 나름대로 독창적인 연구가 뒤따랐다. 633가지의 경우를 모두 손으로 풀 수도 있었지만, 시간을 절약하고 실수를 없애기 위해 컴퓨터를 이용한 것 뿐이다. 왜냐면 똑같은 과정들이 각 경우에 많이 중복되었기 때문에..
곁다리: 프로그램의 옳음을 증명하는 것이 불가능한가 (그리고 괴델에 의해 증명되었는가?)? 그리고 그것이 컴퓨터를 이용한 증명을 반대할 이유가 되는가?
- 괴델(또는 튜링)이 증명한 것은 옳음을 증명하는 것이 불가능한 프로그램이 있다는 것이지, 모든 프로그램의 무오류를 증명할 수 없다는 것은 아니다. 사색문제의 경우 컴퓨터의 증명 과정(?)을 인간이 직접 들여다 볼 수가 없어서 찜찜한 것이지, 프로그램 자체는 거의 검증이 된 상태이다. 그러니 완전히 증명이 되었다고 보아도 무방하다. 어디까지나 인간의 손 -
머리가 아니고 -대신 컴퓨터의 빠른 손을 이용한 것뿐이니까. 찜찜하기로 따지면야 classification of finite groups가 더하다. 전체 논문이 수만 쪽에 이르니 무슨 수로 검증을 하겠는가?
- 또한 괴델의 정리는 임의의 길이와 임의의 크기의 자원을 사용하는 프로그램까지 모두 고려하였을때 그러하다는 것이다. 만약 제한된 크기와 제한된 기억장치 등으로 조건이 주어진다면 불완전성 정리가 허용하지 않는 프로그램을 판단하는 프로그램은 작성이 가능하다.
- 프로그램이 검증이 되었다고 하더라도 함정은 존재한다. 예를 들어 이런 경우를 생각해보자. 프로그램을 작성해서 증명을 수행하는 도중 우주 방사선이 한줄기 날아 들어와서 컴퓨터 메모리 혹은 처리장치의 일정 부분을 교란했다고 해보자. 그리하여 발생한 오류에 의해 사실은 성립하지 않음으로 나올 결과가 성립함으로 나와버렸다고 해보자. 이런 종류의 오류에는 어떻게 대응할 것인가? 프로그램은 커지면 커질 수록 다양한 종류의 외부변수에 의해 간섭받을 것이며 (똑같은 사양의 머신이지만 내 컴퓨터에서만 Windows XP가 돌아가지 않는다!
.png) ) 오류를 출력할 위험성도 높아진다.
) 오류를 출력할 위험성도 높아진다.
이 문제를 해결하는 한 방법은 프로그램을 여러차례, 또 여러가지 다른 조건에서 돌려보아 결과를 비교하는 것이다. 잠깐, 지금 여러차례 다른 조건에서 수행해 결과를 비교한다고 했나? 그것은 전형적인 실험과학이지 수학이 아니다! (우리는 심각한 반례가 있기 전까지 그 결과를 잠정적으로만 신뢰할 수 있다. SeeAlso 과학적방법론)
어떤 수학적 이론도 (공리가 아닌이상) 잠정적으로만 신뢰할 수 있지 않던가요. 또한 공리라 하더라도 다른 계(System)에서는 잘 맞지 않는 이론도 있고. (유명한 유클리드의 제 4공리는 3차원의 세계에서는 맞지 않을수도 있지요. 한 점을 지나고 이 직선과 만나지 않는 직선은 무한개일수도) 수학역시 그런 종류의 문제가 아닌가 생각되네요.-- Arome
이 지적은 일견 타당하지만 간과하고 있는 것이 있다. 그것은 인간의 뇌 또한 또 다른 종류의 컴퓨터에 불과하고 '증명'이란 그 컴퓨터 위에서 돌아가는 프로그램이라는 것이다. 인간의 뇌는 반도체 컴퓨터보다도 오히려 더 많은 오류 가능성에 노출되어 있기 때문에 인류는 오류로부터 프로그램의 수행을 보호하기 위한 장치를 개발했다. 그것은 PeerReview --- 즉, 다른 조건에 있는 또 다른 뇌들이 동일한 알고리즘을 여러차례 수행해서 통계적으로 다수의 결과를 참으로 인정하는 것이다.
그러나, 이런 논리는 강한 상대주의로 흐를 수 있는 심각한 약점을 안고 있다. 과연 수학적 진리란 많은 사람들이 단지 동의하고 있을 뿐인 것인가 아니면 그 이상인가?
이런 논법이라면 굳이 "수학적"이란 수식어도 필요없죠.
수학적인 것은 어떤것인지요?
"인간의 뇌가 만든" 논리학으로 "인간에 의해서" 증명이 가능해야지 수학적인 정리입니다. 인간에 의한 것이기 때문에 천재성의비밀이라는 책에서처럼 수학이 생물학으로 흐를 수도 있습니다.
그러니까.. 저 지도의 다섯 나라는 과거에 모두 한나라 였었습니다. 그러나 민족분열 때문에 내전이 발생했고 급기야 다섯나라로 분열되고 말았죠. 그런데 지도상의 B`이라는곳은 B라는 나라와 같은 민족이였기 때문에 B라는 나라에 속하게 되었습니다.
분명 같은나라는 같은색이 칠해져야 하고 그러면 저 경우에는 4개의 색으로는 절대 표현할 수 없게 됩니다.
4색문제는 "같은 나라를 같은 색으로 칠하는 문제"가 아니라 "인접한 지역을 다른 색으로 칠하는 문제"입니다. 즉, B'와 B가 같은 나라든 아니든 간에 같은 색으로 칠해야할 이유가 없습니다. B는 C와 같은 색으로 칠하고, B'는 D나 A와 같은 색으로 칠하면 위 그림은 4색문제를 만족합니다.쓴귤
같은 나라끼리는 같은 색을 칠해야 하는 데 나라가 이미 5개있으니 5개의 색을 써야 겠죠. --RedPain
그냥 고등학교 시절 공부하기 싫은 학생의 망상이였을지도.. 자운원같은 나라끼리는 같은 색을 칠해야 하는 데 나라가 이미 5개있으니 5개의 색을 써야 겠죠. --RedPain
같은 나라가 위처럼 둘로 떨어지는 경우에는 12색이면 충분합니다. 그리고 최소한 9색이 필요한 경우도 알려져 있습니다.